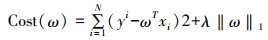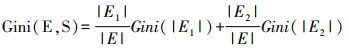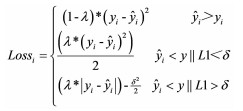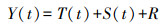传染病的发病一直是一个备受关注的公共卫生问题,为社会、经济和健康带来了巨大负担[1]。利用传染病数据预测传染病的趋势可为实际的防控工作提供重要的指导和方向[2]。既往研究中常使用时间序列方法以预测传染病发病率,如季节性自回归差分移动平均模型(seasonal autoregressive integrated moving average,SARIMA)[3],以及适用于处理非线性数据的非自回归(non-autoregressive,NAR)模型[4],长短期记忆递归神经网络(long short term memory,LSTM)[5]等。相较于线性模型,非线性模型可更好地拟合时间序列中非周期性的随机波动[6-7]。对于传染病的时间序列预测,可考虑使用多个模型进行融合分析,其中部分模型用于拟合传染病的趋势和季节性,其他模型则利用外部相关数据对残差项进行校准,继而提升预测精度[8-9]。
影响传染病发病的因素较为复杂,既往传染病预测研究主要关注于不同病种和地区之间的差异[10]。随着卫星遥感和互联网技术的发展,获取和利用传染病相关的多源数据成为可能。当前,已有一些既往研究在传染病预测中成功应用了互联网数据,这揭示了互联网数据在预测传染病时的先行性和相关性[11-13]。因此,综合利用多源数据可明显提高预测模型的效果和准确性。
参数优化和损失函数是确保机器学习方法准确性的关键步骤。然而,传统算法常常面临收敛速度慢和易陷入局部最优等问题[14]。为了应对这些挑战,元启发式算法被广泛应用以有效优化模型参数,提高寻找全局最优解的能力[15],如粒子群算法(particle swarm optimization,PSO)和星雀优化算法(nutcracker optimizer algorithm,NOA)等[16]。另外,在处理不同类型的数据时,选择适合的损失函数进行校正也非常重要[17]。
病毒性肝炎发病率较高的一类法定传染病,其在时间序列上具有明显的特征[18]。因此,本研究以重庆市的肝炎数据集为基础,针对发病率的预测模型进行了有效性和通用性的研究。在这项研究中,我们提出了一种新的时间序列神经网络模型,其通过在预测模型中异步地引入多源数据和历史发病率,可有效提高预测的准确性。之后,本研究还引入了超参数和损失函数优化,并将该模型命名为时滞输入神经网络+(delayed input neural network+,DINN+),旨在充分提取时间序列信息及发现输入变量与发病率之间的相关性。
本文使用重庆市肝炎数据集进行了实证研究,并在以下方面进行了创新:①多样方法:DINN+通过残差方式进行方法融合,聚焦于传统季节分解模型中无法识别的部分,利用元启发算法进行参数优化。针对传染病数据的特点,提出了针对性的联合四分位-Huber损失函数(joint quantile Huber loss,JQHL)联合损失函数。②多源数据:DINN+整合了传染病数据、大气污染物数据、气候数据、网络指数和股票指数等多源数据,这有利于修正传染病数据的预测结果,并提升模型对扰动部分的预测能力。③应用价值:DINN+丰富和补充了传染病预测的方法学研究内容,其可作为未来传染病预测的全新基准,并为各类传染病发病预测提供参考依据。
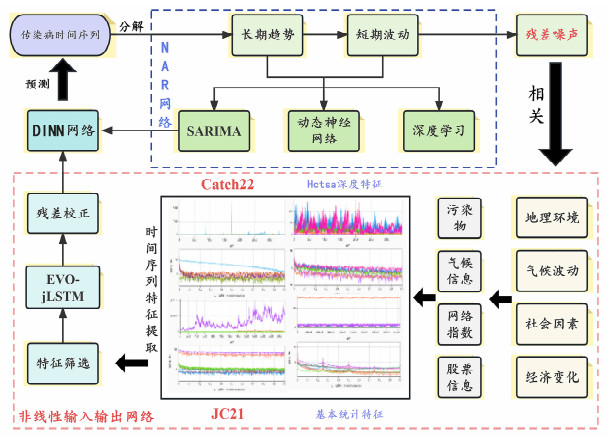
1 材料与方法全文的技术路线如图 1所示。DINN+的整体结构为多输入、单输出的时序分析模型。
|
| 注:蓝色虚线框代表利用历史数据进行时序分析的NAR网络的部分,红色虚线框代表利用多源数据进行残差校正的部分。 图 1 全文技术路线图 |
1.1 数据来源和特征提取
重庆市肝炎月发病率数据来源于中国卫生疾控中心数据库。原始数据包含了甲、乙、丙、丁、戊和未定型6种类型的病毒性肝炎在重庆市每月的发病报告人数。为了计算当月的发病率(每10万人),将报告人数除以当年重庆市的统计人口数(以10万为单位)。大气污染物数据来源于中国环境监测总站官网,气候数据来源于国家气象星系中心。网络指数数据来源于百度搜索引擎。研究数据的时间跨度均为2013年11月至2023年5月,共计115个月,涵盖46个变量。为获得指数信息,主要通过数据库进行关键词共现性分析、专家共识及经验确定与待分析传染病相关性较高的关键词信息。然后,利用搜索引擎将这些关键词与文本数据进行匹配,进而获取关键词的文本指数信息。所有研究数据均经过合理的收集,传染病月发病率数据中无缺失现象。
影响传染病发病趋势的因素很多,包括地理环境、气候波动、社会因素和经济变化等。一项流感流行趋势的研究揭示,低社会经济地位的人群更容易感染流感[19]。此外,股票市场的波动与社会经济变化紧密相关,其有利于及时、有效地反映经济动态的变化。因此,本文计划将相关股票指数纳入研究,通过该指标反映社会和个体层面在经济变化方面的情况。
因此,除肝炎发病率外,本研究还纳入了45个其他具体指标。其中,污染物信息、百度指数和股票指数均为按日统计的,而气候数据为每3小时监测一次。因此,需要进行时间序列特征提取,以获取每个指标在每个月的时间序列特性。使用了Catch22[20]和JC21方法进行特征提取,特征提取结果如表 1所示。每个变量提取了43个时序特征,共衍生出1 935个变量。
| 类别 | 具体指标 |
| 地理环境 | PM2.5、PM10、SO2、CO、NO2、O3 |
| 气候 | 温度、气压、风向、风速、能见度、露点温度、降水量 |
| 社会因素 | 百度搜索指数(传染、肝炎、肝炎症状、肝炎治疗、疫苗) |
| 经济变化 | 上证指数、深证成指、创业板(开盘、最高、最低、收盘、涨跌、涨幅、振幅、总手、金额) |
| Catch22 | DN_HistogramMode_5、DN_HistogramMode_10、CO_f1ecac、CO_FirstMin_ac、CO_NonlinearAutocorr、CO_trev_1_num、MD_hrv_classic_pnn40、SB_BinaryStats_mean_longstretch1、DN_MinMax、DN_nlogL_norm、EN_ApEn、IN_AutoMutualInfoStats_40_gaussian_fmmi、FC_LocalSimple_mean1_tauresrat、DN_OutlierInclude_p_001_mdrmd、DN_Quantile、SP_Summaries_welch_rect_area_5_1、SB_BinaryStats_diff_longstretch0、CR_RAD、SC_FluctAnal_2_rsrangefit_50_1_logi_prop_r1、SC_FluctAnal_2_dfa_50_1_2_logi_prop_r1、SP_Summaries_welch_rect_centroid、DN_HighLowMu(y) |
| JC21 | 最大值、最小值、平均值、峰-峰值、整流平均值、有效值、峰值、方差、标准差、峭度、偏度、均方根、波形因子、峰值因子、脉冲因子、裕度因子、重心频率、均方频率、频率方差、频带能量、相对功率谱熵 |
1.2 特征选择
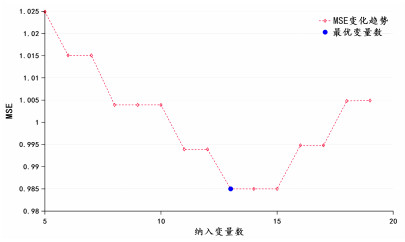
首先,采用最小绝对值选择与收缩算子(least absolute shrinkage and selection operator,LASSO)回归(式1)进行了变量初筛,以去除无效变量和共线性变量,最终筛选出了47个有价值的时序特征[21]。接着,使用随机森林(式2)对这些特征进行了重要性排序,并根据变量选择的迭代情况(见图 2)选出13个重要性较高的特征作为外部输入变量,继而纳入后续的研究模型中。
|
| 图 2 变量选择变化趋势图 |
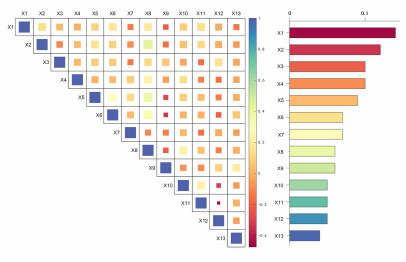
热力图分析结果和重要性排序如图 3所示,其中X1至X13分别代表Catch7_CO、Catch15_肝炎症状、JC-17-PM10、JC-17-SO2、JC-7-O3、JC-20-O3、JC-1-肝炎症状、JC-16-肝炎治疗、JC-5-疫苗、JC-13-温度、Catch-4-创指收盘、Catch-5-深成指涨跌、JC-2-创指开盘。
|
| 图 3 热力图与重要性排序 |
1.3 联合损失函数
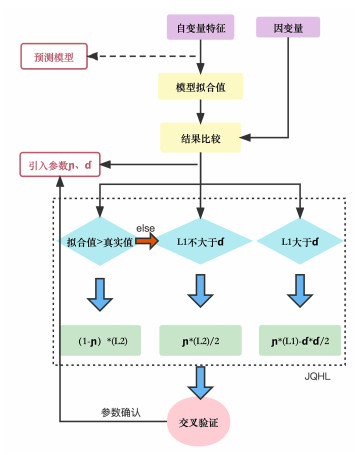
常用的Huber损失函数有利于综合衡量均方误差(mean-square error,MSE)、平均绝对误差(mean absolute error,MAE)的优势[17, 22],而分位数损失函数则根据拟合值和真实值的关系以调整权重[23]。鉴于此,本文提出了一种新的联合分位数-Huber损失函数(joint quantile Huber loss,JQHL),该函数结合了分位数损失函数和Huber损失函数的优点,其算法流程如图 4所示。
|
| 图 4 JQHL的算法流程图 |
依据式4,λ值代表了联合损失函数中各部分的权重。在实际应用中,可通过设置λ的大小以调整损失函数中各部分的重要性。当λ取值较大且δ取值较小时,适用于存在极值点且极值点接近于0的数据。当λ取值较小时,适用于数据分布较为规整的情况。而当λ取值较大且δ取值较大时,则适用于存在极值点且极值点明显偏大的情况。算法1展示了JQHL的伪代码。
1.4 参数优化在机器学习和深度学习中,参数优化是影响算法性能和准确性的关键步骤[24]。然而,模型融合和损失函数改进会增加超参数的数量,手动调参很难取得良好的结果。因此,需要选择适合的优化算法以兼顾运行性能和效率。
对常用的元启发式算法进行测试函数比较后,本文筛选出了NOA算法。该算法具有高效的全局搜索能力、自适应的搜索策略、并行计算能力、鲁棒性强和可解释性强等优点[16]。因此,本文选择引入NOA算法以自动优化模型的超参数和损失函数的系数,以期对模型精确度进行有效提升。
1.5 改良预测模型鉴于不同的模型可有效捕捉到数据中不同的特征和特点,本文考虑串联模型融合以提供更全面、准确的特征表示能力[25]。为提高传染病发病趋势预测模型的精确度和泛化能力,需要构建适合的独立模型来协作完成每个预测步骤。因此,本文所提的DINN基于NAR和LSTM两种模型而提出。具体而言,本文构建了一个NAR模型以进行传染病的自回归拟合,并将延迟输入的多变量特征引入到融合模型中。在该过程中,使用由自回归模型得出的残差序列作为下一步LSTM模型的因变量。通过利用与传染病相关的多源数据来拟合残差项,本文规避了同时输入所引起的时间序列分解项之间的影响,并降低了自回归过程与变量拟合过程之间的相互干扰。
一方面,选用神经网络以拟合和训练NAR模型,并采用贝叶斯优化算法对NAR模型的参数进行估计和优化,这有利于提升模型拟合训练数据的性能。NAR的算法原理可表达为
另一方面,使用多输入长短期记忆递归神经网络(multiple input long short term memory,MI-LSTM)处理多输入特征的序列数据[26]。通过收集肝炎相关的地域多源数据作为输入特征,为每个输入特征定义一个单独的输入层,并将它们连接到LSTM模型中。将多个LSTM层进行堆叠,以便在时间序列上逐步处理输入数据,并且每个LSTM层的输出作为下一层的输入[27]。最后,将LSTM模型的输出连接至一个或多个全连接层,以生成所需的预测。
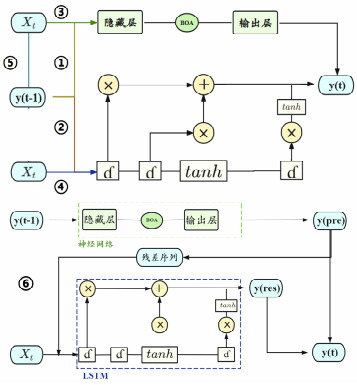
在DINN模型的基础上,本文还加入了“1.3联合损失函数”和“1.4参数优化”中提及的两处改进,继而构建出DINN+。为进行模型性能的比较,本文还纳入了SARIMA及NARX模型。本研究所用各模型的构建流程如图 5所示。其中,Xt表示肝炎发病率时间序列。
|
| 注:通路①代表NAR模型;通路②代表LSTM模型;通路③代表非线性输入输出模型;通路④代表Mi-LSTM模型;通路⑤代表NARX模型;通路⑥代表DINN模型。 图 5 本文纳入各个模型的构建流程 |
1.6 模型训练和评价
为便于数据处理和加快模型收敛速度,同时规避不同量纲对结果准确度的影响,对数据进行了[0, 1]标准化处理,继而使数据符合标准正态分布。此外,纳入从2013年11月到2022年5月的数据作为训练集,共计103个月;预测集则包括2022年6月到2023年5月的数据,共计12个月。本研究利用MATLAB 2023a进行了模型构建、指标计算和绘图等工作。
纳入五种常见的评价指标以评估模型的性能,包括均方误差(MSE)、平均绝对误差(MAE)、均方根误差(root-mean-square error,RMSE)、平均绝对百分比误差(mean absolute percentage error,MAPE)和拟合优度(R-square,R2)。前4个指标用于衡量模型的拟合误差,而R2则表示模型对实际数据趋势的拟合程度。较小的误差值表示模型的拟合性能较好,较大的R2值则表示模型对实际数据趋势的预测能力较强。
2 结果在结果部分,首先分析比较了优化算法的性能。随后,逐步评估单输入模型、同步多输入模型和时滞输入神经网络的预测结果,最终揭示本文所提DINN+的优越性。
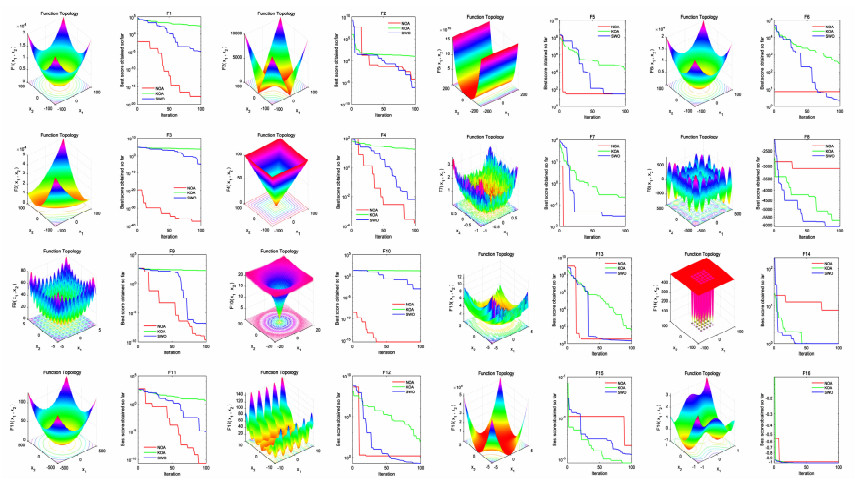
2.1 优化算法性能比较以开普勒优化算法(Kepler optimization algorithm,KOA)[28]和蜘蛛蜂优化算法(spider wasp optimizer,SWO)[29]作为对照,使用16种常见的标准测试函数对各优化算法进行性能分析。结果显示,NOA算法在大多数测试函数中均表现出了更快的整体收敛速度和更强的全局寻优能力,如图 6所示。因此,将NOA作为DINN+的首选算法。
|
| 注:NOA为红线、对照为蓝线,折线图展示了基准函数第一维第一个解的收敛趋势。 图 6 NOA的算法性能测试 |
2.2 单输入模型预测结果
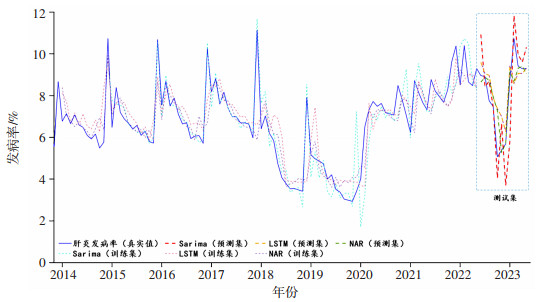
单输入模型指利用时间序列的历史数据以预测未来趋势的模型。NAR的MSE、MAE、RMSE和MAPE均低于SARIMA和LSTM;而R2高于其他模型,在测试集上达到了0.708 7,表现出了优异的预测性能。三种模型在训练集和测试集上的拟合效果展示于图 7。
|
| 注:训练集数据为2013年11月至2022年5月,测试集数据为2022年6月至2023年5月。 图 7 各类单输入模型的拟合结果 |
2.3 同步多输入模型预测结果
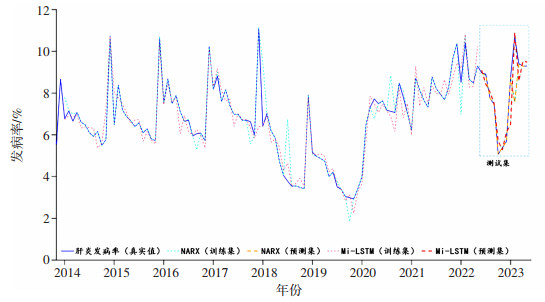
使用筛选出的13类特征结合肝炎发病率时间序列,构建了同步输入的NARX模型和Mi-LSTM模型,并对重庆市的肝炎发病率进行了校正预测分析。结果表明:相较于前述单输入模型,Mi-LSTM模型在性能上取得了较大提升,测试集R2达到了0.810 4。两种同步多输入模型在训练集和测试集上的拟合效果如图 8所示。
|
| 注:训练集数据为2013年11月至2022年5月,测试集数据为2022年6月至2023年5月。 图 8 同步多输入模型拟合图 |
2.4 时滞输入神经网络的预测结果
相较于对比模型,DINN模型在各项指标上均获得了不同程度的提升。在测试集上,DINN模型的MSE、MAE、RMSE和MAPE均低于其他模型,而R2则优于其他模型。具体而言,DINN模型的R2值为0.842 4。通过延时纳入多源数据衍生的时序特征,DINN模型可充分发挥NAR模型和LSTM模型的优势,显著提升模型的总体预测能力,减小预测值与实际值之间的差距。
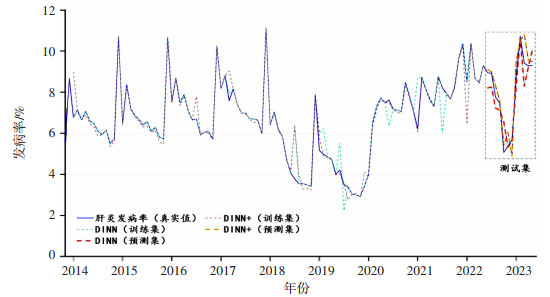
在DINN模型的基础上优化的DINN+的预测结果如表 2、图 9所示。研究结果表明,参数优化算法和联合损失函数的引入有利于有效修正预测结果,进而获得更精确的预测效果。因此,DINN+模型是重庆市肝炎发病率趋势预测的最优模型。
| 模型 | 数据集 | MSE | MAE | RMSE | MAPE | R2 |
| SARIMA | 训练集 | 0.096 6 | 0.597 1 | 0.916 2 | 0.098 1 | 0.777 7 |
| 测试集 | 0.400 1 | 1.138 2 | 1.386 1 | 0.152 6 | 0.364 3 | |
| LSTM | 训练集 | 0.108 2 | 0.742 5 | 1.087 3 | 0.114 9 | 0.653 1 |
| 测试集 | 0.330 5 | 0.863 1 | 1.144 8 | 0.125 2 | 0.566 4 | |
| NAR | 训练集 | 0.105 4 | 0.678 0 | 1.058 8 | 0.101 9 | 0.671 0 |
| 测试集 | 0.270 9 | 0.587 5 | 0.938 3 | 0.081 2 | 0.708 7 | |
| NARX | 训练集 | 0.053 1 | 0.151 7 | 0.528 6 | 0.027 8 | 0.919 6 |
| 测试集 | 0.265 2 | 0.271 6 | 0.918 5 | 0.025 5 | 0.720 9 | |
| Mi-LSTM | 训练集 | 0.065 9 | 0.388 5 | 0.662 7 | 0.057 4 | 0.871 1 |
| 测试集 | 0.218 5 | 0.485 8 | 0.757 0 | 0.062 0 | 0.810 4 | |
| DINN | 训练集 | 0.049 9 | 0.136 5 | 0.502 0 | 0.026 8 | 0.926 1 |
| 测试集 | 0.199 2 | 0.537 9 | 0.690 1 | 0.072 0 | 0.842 4 | |
| DINN+ | 训练集 | 0.045 6 | 0.190 4 | 0.458 7 | 0.034 5 | 0.938 3 |
| 测试集 | 0.170 9 | 0.461 2 | 0.592 1 | 0.062 6 | 0.884 0 |
|
| 注:训练集数据为2013年11月至2022年5月,测试集数据为2022年6月至2023年5月。 图 9 时滞输入模型拟合图 |
3 讨论
本文在重庆市肝炎发病率的分析与预测中进行了一系列研究。首先,本文进行了比较研究,评估了三种单输入模型和两种同步多输入模型。在这个基础上,本文提出了外部多变量迟输入和模型融合策略,并通过结合元启发式优化算法,进一步改进了损失函数的设计。最终,本文成功构建了最优的融合模型DINN+,在测试集上展现了最佳的预测性能。
基于NAR和LSTM,本研究构建了DINN模型,在预测重庆市肝炎发病中取得了较好的性能。相较于传统的线性自回归模型,NAR模型可探索数据之间的复杂关联和非线性模式,并通过选择适当的非线性激活函数和网络结构以适应不同数据的特点[30]。这种灵活性使得NAR模型对各类时间序列数据的适应性较好,并且可更好地捕捉数据的特征,进而提供更准确的预测结果[31-32]。LSTM通过使用门控机制以控制信息的流动,从而可更好地处理长期依赖性[33]。在多变量输入中,每个变量可作为LSTM网络中的一个输入维度,有助于提供更丰富的信息以增强预测能力[34-35]。本研究构建的DINN模型可有效地对时间序列的各部分进行分步预测,其利用NAR模型以捕捉肝炎发病的趋势和周期,同时使用Mi-LSTM模型分析外部多因素对传染病流行趋势的影响,充分发挥了两种模型的各自优势。因此,NAR模型可聚焦于分析肝炎发病的趋势,而Mi-LSTM模型则可专注于寻找外部多因素对肝炎发病趋势造成的扰动,从而提高预测的精度。通过将NAR模型和Mi-LSTM模型串联起来,能够更好地发挥它们各自的优势。
本研究在DINN模型的基础上进行了进一步优化和改良,引入了参数优化和改良的损失函数,从而构建了DINN+模型。针对数据的特点,我们提出了JQHL联合损失函数,使模型能够更关注发病率数据的集中部分,并尽可能避免离群值的影响。为解决模型融合和损失函数优化增加的超参数问题,本文引入了NOA元启发优化算法,进一步提高了模型的准确性和泛化性能。损失函数优化和参数寻优有利于进一步提升模型性能,分析原因在于,DINN模型中外部多因素变量的延迟输入有助于规避历史发病率数据与输入变量之间的相互影响。研究结果表明,相较于单输入模型和同步多输入模型,DINN模型在预测准确性方面表现出更好的性能。
随着外部干扰因素的增加,仅使用传染病历史数据预测未来趋势具有较大的局限性[36]。以谷歌流感指数为代表的互联网检索数据已被逐渐应用于传染病预测的领域[13]。互联网指数可有效反映人群的互联网行为,对人群在传染病发病前的自发性和先行性检索行为进行合理评估。大气污染物数据可有效反映当地环境变化对人群罹患传染病概率的影响。气候数据在一定程度上可反映天气变化对人群迁徙的影响,从而影响传播途径和疾病发病率。从经济水平变化的角度,股票指数可有效地代表社会经济变化对疾病发生发展特点的干扰。因此,将这四种类型的网络数据作为外部多变量输入,通过Mi-LSTM模型对肝炎发病率残差项进行拟合,这有利于提升模型的准确性。
本研究虽然在设计和执行上合理且严格,但仍有改进和提升的空间。对未来的研究方向展望如下。首先,从多个维度、广泛的领域分析空间分布、人群分布和致病因素等特征,以提高预警效果。其次,通过理论研究和探索特征选择方法,如递归消除法、相关系数法、随机森林,构建适用于传染病数据的特征选择方法,提高预测效果。最后,应在多个传染病数据集上验证DINN模型的泛化能力。通过这些研究方向,有望提升研究成果,对传染病预测领域做出更大贡献。
综上所述,本研究利用多源网络大数据作为外部输入变量进行重庆市肝炎发病率的预测。在NAR模型和Mi-LSTM模型的基础上引入了联合损失函数和参数优化算法,成功构建了DINN+模型,并经实证研究揭示了其预测性能的优异性。因此,本研究提出的DINN+模型具有较好的预测性能,并可为传染病的防控提供有力的指导。
| [1] |
YI D, CHEN X, WANG H, et al. COVID-19 epidemic and public health interventions in Shanghai, China: Statistical analysis of transmission, correlation and conversion[J]. Front Public Health, 2023, 10: 1076248. |
| [2] |
XU B, LI J, WANG M. Epidemiological and time series analysis on the incidence and death of AIDS and HIV in China[J]. BMC Public Health, 2020, 20(1): 1906. |
| [3] |
MAHMOUDI M R, BAROUMAND S. Modeling the stochastic mechanism of sensor using a hybrid method based on seasonal autoregressive integrated moving average time series and generalized estimating equations[J]. ISA trans, 2022, 125: 300-305. |
| [4] |
EIKENBERRY S E, MARMARELIS V Z. A nonlinear autoregressive Volterra model of the Hodgkin-Huxley equations[J]. J Comput Neurosci, 2013, 34(1): 163-183. |
| [5] |
LIU X, LIU C, HUANG R, et al. Long short-term memory recurrent neural network for pharmacokinetic-pharmacodynamic modeling[J]. Int J Clin Pharmacol Ther, 2021, 59(02): 138-146. |
| [6] |
DI NUNNO F, RACE M, GRANATA F. A nonlinear autoregressive exogenous (NARX) model to predict nitrate concentration in rivers[J]. Environ Sci Pollut Res Int, 2022, 29(27): 40623-40642. |
| [7] |
WANG Y, XU C, WANG Z, et al. Time series modeling of pertussis incidence in China from 2004 to 2018 with a novel wavelet based SARIMA-NAR hybrid model[J]. PLoS One, 2018, 13(12): e0208404. |
| [8] |
IMAI C, ARMSTRONG B, CHALABI Z, et al. Time series regression model for infectious disease and weather[J]. Environ Res, 2015, 142: 319-327. |
| [9] |
MESSACAR K, PARKER S K, TODD J K, et al. Implementation of rapid molecular infectious disease diagnostics: the role of diagnostic and antimicrobial stewardship[J]. J Clin Microbiol, 2017, 55(3): 715-723. |
| [10] |
REICH N G, LAUER S A, SAKREJDA K, et al. Challenges in real-time prediction of infectious disease: A case study of dengue in Thailand[J]. PLoS Negl Trop Dis, 2016, 10(6): e0004761. |
| [11] |
YADAV S K, AKHTER Y. Statistical modeling for the prediction of infectious disease dissemination with special reference to COVID-19 Spread[J]. Front Public Health, 2021, 9: 645405. |
| [12] |
ROMERO-ALVAREZ D, PARIKH N, OSTHUS D, et al. Google health trends performance reflecting dengue incidence for the Brazilian states[J]. BMC Infect Dis, 2020, 20(1): 252. |
| [13] |
GAO C, ZHANG R, CHEN X, et al. Integrating Internet multisource big data to predict the occurrence and development of COVID-19 cryptic transmission[J]. NPJ Digit Med, 2022, 5(1): 161. |
| [14] |
ZHANG R, GAO C, CHEN X, et al. Genetic algorithm optimised Hadamard product method for inconsistency judgement matrix adjustment in AHP and automatic analysis system development[J]. Expert Syst Appl, 2023, 211: 118689. |
| [15] |
MARTÍNEZ-ÁLVAREZ F, ASENCIO-CORTÉS G, TORRES J F, et al. Coronavirus optimization algorithm: A bioinspired metaheuristic based on the COVID-19 propagation model[J]. Big Data, 2020, 8(4): 308-322. |
| [16] |
ABDEL-BASSET M, MOHAMED R, JAMEEL M, et al. Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems[J]. Knowl Based Syst, 2023, 262: 110248. |
| [17] |
SPELLER J, STAERK C, MAYR A. Robust statistical boosting with quantile-based adaptive loss functions[J]. The Int J Biost, 2023, 19(1): 111-129. |
| [18] |
SUMI A, LUO T, ZHOU D, et al. Time-series analysis of hepatitis A, B, C and E infections in a large Chinese city: application to prediction analysis[J]. Epidemiol Infect, 2013, 141(5): 905-915. |
| [19] |
SLOAN C, CHANDRASEKHAR R, MITCHEL E, et al. Socioeconomic disparities and influenza hospitalizations, Tennessee, USA[J]. Emerg Infec Dis, 2015, 21(9): 1602-1610. |
| [20] |
LUBBA C H, SETHI S S, KNAUTE P, et al. catch22: CAnonical Time-series CHaracteristics: Selected through highly comparative time-series analysis[J]. Data Min Knowledge Discovery, 2019, 33(6): 1821-1852. |
| [21] |
WU L, ZHOU B, LIU D, et al. LASSO regression-based diagnosis of acute ST-segment elevation myocardial infarction (STEMI) on electrocardiogram (ECG)[J]. J Clin Med, 2022, 11(18): 5408. |
| [22] |
HAZARIKA B B, GUPTA D. Random vector functional link with ε-insensitive Huber loss function for biomedical data classification[J]. Comput Methods Programs Biomed, 2022, 215: 106622. |
| [23] |
LOPEZ-MARTIN M, SANCHEZ-ESGUEVILLAS A, HERNANDEZ-CALLEJO L, et al. Additive ensemble neural network with constrained weighted quantile loss for probabilistic electric-load forecasting[J]. Sensors, 2021, 21(9): 2979. |
| [24] |
YE W, CHEN X, LI P, et al. OEDL: an optimized ensemble deep learning method for the prediction of acute ischemic stroke prognoses using union features[J]. Front Neurol, 2023, 14: 1158555. |
| [25] |
WANG K W, DENG C, LI J P, et al. Hybrid methodology for tuberculosis incidence time-series forecasting based on ARIMA and a NAR neural network[J]. Epidemiol Infect, 2017, 145(6): 1118-1129. |
| [26] |
LISMAN J. Glutamatergic synapses are structurally and biochemically complex because of multiple plasticity processes: long-term potentiation, long-term depression, short-term potentiation and scaling[J]. Philos Trans R Soc Lond B Biol Sci, 2017, 372(1715): 20160260. |
| [27] |
BAI Y, ZENG B, LI C, et al. An ensemble long short-term memory neural network for hourly PM2.5 concentration forecasting[J]. Chemosphere, 2019, 222: 286-294. |
| [28] |
ABDEL-BASSET M, MOHAMED R, AZEEM S A A, et al. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler's laws of planetary motion[J]. Knowl Based Syst, 2023, 268: 110454. |
| [29] |
ABDEL-BASSET M, MOHAMED R, JAMEEL M, et al. Spider wasp optimizer: a novel meta-heuristic optimization algorithm[J]. Artif Intell Rev, 2023, 56(10): 11675-11738. |
| [30] |
KIRBAŞ I, SOZEN A, TUNCER A D, et al. Comparative analysis and forecasting of COVID-19 cases in various European countries with ARIMA, NARNN and LSTM approaches[J]. Chaos Solitons Fractals, 2020, 138: 110015. |
| [31] |
CARREON-ORTIZ H, VALDEZ F, MELIN P, et al. Architecture optimization of a non-linear autoregressive neural networks for Mackey-glass time series prediction using discrete mycorrhiza optimization algorithm[J]. Micromachines, 2023, 14(1): 149. |
| [32] |
YU L, ZHOU L, TAN L, et al. Application of a new hybrid model with seasonal auto-regressive integrated moving average (ARIMA) and nonlinear auto-regressive neural network (NARNN) in forecasting incidence cases of HFMD in Shenzhen, China[J]. PloS One, 2014, 9(6): e98241. |
| [33] |
MIAO R, ZHANG B. Analysis on time-series data from movie using MF-DCCA method and recurrent neural network model under the internet of things[J]. Comput Intell Neurosci, 2022, 2022: 7400833. |
| [34] |
HATAMI N, CHO T H, MECHTOUFF L, et al. CNN-LSTM Based multimodal MRI and clinical data fusion for predicting functional outcome in stroke patients[C/OL]//2022 44th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC). Glasgow: IEEE, 2022: 3430-3434[2022-10-05]. https://ieeexplore.ieee.org/document/9871735/. DOI: 10.1109/EMBC48229.2022.9871735.
|
| [35] |
CHEN S, ZOU Y, LIU P X. IBA-U-Net: Attentive BConvLSTM U-Net with Redesigned Inception for medical image segmentation[J]. Comput Biol Med, 2021, 135: 104551. |
| [36] |
Global Burden of Disease 2021 Health Financing Collaborator Network. Global investments in pandemic preparedness and COVID-19: development assistance and domestic spending on health between 1990 and 2026[J]. Lancet Glob Health, 2023, 11(3): e385-e413. |