爆炸武器在现代战争中被广泛应用。颌面部由于缺少防护,导致颌面部爆炸伤比例较高,且颌面部爆炸伤救治困难,致伤及致死率较高。建立人颌面部软硬组织爆炸伤模型和系统分析颌面部爆炸伤致伤机制、损伤特点、防护与救治要点是颌面部战创伤研究的重点[1]。三维有限元法(three-dimensional finite element method,FEM)能够分析物体间及物体内部的复杂力学变化,预测力学作用的效应,可应用于颌面部爆炸伤模型研究,是颌面部战创伤模型研究常用的方法。课题组前期已将FEM应用于颌面部骨组织的火器伤、爆炸伤、撞击伤的研究[2-5],取得良好实验效果。但是FEM在爆炸伤研究中具有一定局限性,表现为在模拟高速大变形时,容易出现网格过度畸变,从而导致计算出错或结果不可靠,而光滑粒子动力学方法(smoothed particle hydrodynamics,SPH)可弥补FEM研究的不足。
SPH的基本思想是将复杂的颌面部软硬组织三维形状离散成有限个带质量的粒子,粒子之间不需要单元网格连接,而是通过核函数将它们联系起来,物理性质全部分配在粒子上,由各个粒子表现出力学性质,并由此模拟不同粒子之间的相互作用,从而避免了FEM研究中单元格畸变和负体积的产生[6]。近年来,SPH方法在生物力学仿真研究中得到应用[7-14],但大多集中于血液流体模拟,对于软硬组织爆炸损伤生物力学模拟,则鲜见相关研究报道。
本研究拟建立人下颌软硬组织爆炸伤SPH模型,分析人下颌软硬组织爆炸伤致伤过程及生物力学特点,对比研究SPH和FEM方法在人下颌软硬组织爆炸伤模型中的有效性,为颌面部软硬组织爆炸伤模型研究提供新方法。
1 资料与方法 1.1 实验设备与软件实验设备:64排双螺旋CT(General Electric, 美国);Signa HD×3.0T MRI (General Electric,美国);电脑:处理器Intel i7-7700K,八核,4.20 GHz,内存16 G,硬盘1 TB。仿真模拟软件:MIMICS 17.0 (Materialise公司,比利时);有限元处理软件:HyperMesh2017(美国Altair公司);仿真运算求解软件:LS-DYNA971R8.0.0(LSTC公司,美国);编程软件:Microsoft Visual Studio 2013(美国微软公司);Intel Visual Fortran 2013(美国Intel公司)。
1.2 人下颌软硬组织SPH和FEM模型的建立健康成年男性(26岁,身高171 cm,体质量65 kg,签署知情同意书)在陆军军医大学第二附属医院放射科行CT和MRI扫描,扫描范围为颅顶至第5颈椎层面,扫描层厚为0.625 mm,分辨率为512×512像素,像素大小0.533 mm,共获得数据393张,将数据以医学数字图像和通讯格式导入MIMICS 17.0进行下颌骨、咬肌三维模型建立。
1.3 FEM模型的建立利用MIMICS软件中阈值分割功能,从数据中提取下颌骨和咬肌模型,建立咬肌-下颌骨软硬组织三维模型,将模型进行面网格划分, 然后导入HyperMesh软件中进行体四节点四面体网格划分,并设置单元格尺寸为3 mm,最后生成FEM咬肌-下颌骨实体网格模型。
1.4 SEM模型的建立将建立的咬肌-下颌骨软硬组织三维模型,通过编程软件Microsoft Visual Studio和Intel Visual Fortran采用Fortran语言将模型离散成SPH粒子,设定粒子间距为3 mm,各粒子在三维空间中离散均匀分布。下颌骨和咬肌的模型设置与FEM一致,只是将FEM中的网格节点处建成SPH粒子。
1.5 人下颌软硬组织爆炸伤SPH和FEM模拟选取TNT炸药为致伤物,爆炸目标为左侧下颌角中点,爆炸距离为3 cm,其中TNT炸药密度为1 590 kg/m3,1 000 mg的TNT炸药体积为628.93 mm3,在ANSA软件中创建炸药几何形态,并划分为八节点四面体网格。建立空气域四节点四面体网格,将炸药及颌面部软硬组织网格全部包围在内,从而建立人下颌软硬组织爆炸伤FEM模型。通过编程软件建立TNT炸药的粒子模型,并设定炸药粒子间距为0.5 mm,共得到粒子5 832个,在SPH方法中,TNT爆炸粒子产生的冲击波可以直接传递并作用于人软硬组织SPH粒子,爆炸冲击波不必通过空气域传播,因此SPH爆炸伤模型不需要对空气域设置。选取FEM和SPH模型中左侧下颌角中点为研究目标,分别绘制爆炸冲击波对下颌骨、咬肌的应力-时间变化曲线。
1.6 FEM模型材料属性设置在LS-DYNA程序中,下颌骨组织采用分段线性弹塑性材料模型*MAT_PIECEWISE_LINEAR_PLAST-ICITY,咬肌采用各向同性黏弹性材料模型*MAT_VISCOELASTIC,并根据*MAT_ADD_EROSION设置相应的失效应变,TNT炸药采用高爆材料模型*MAT_HIGH_EXPLOSIVE_BURN,并设置状态方程*EOS_JWL,空气采用空材料模型*MAT_NULL和状态方程*EOS_LINEAR_POLYNOMIAL进行模拟,模型材料参数见表 1。为了仿真骨、咬肌受力变形断裂的情况,节点约束的失效方式设定为应变失效,失效值为0.08[15]。将完成参数设定及算法设定的人下颌软硬组织爆炸伤FEM模型导入有限元运算软件LS-DYNA[16]中,选用LS-DYNA程序中的* CONTACT_ERODING_NODES_TO_SURFACE运算。
| 材料 | 密度/g·cm-3 | 体积模量/MPa | 长剪切模量/MPa | 短剪切模量/MPa | 衰减系数/ ms-1 | |||
| 咬肌 | 1.040 | 5 | 0.016 8 | 0.052 8 | 0.035 | |||
| 材料 | 杨氏模量/MPa | 泊松比 | 密度/g·cm-3 | 屈服应力/MPa | 失效应变(%) | |||
| 皮质骨 | 13 700 | 0.3 | 1.74 | 50.0 | 0.44 | |||
| 松质骨 | 1 370 | 0.3 | 0.70 | 1.8 | 1.50 | |||
| 材料 | A/GPa | B/GPa | R1 | R2 | E/Gpa | D/m·s-1 | ω | ρ/kg·m-3 |
| TNT炸药 | 679 | 11.88 | 4.54 | 0.98 | 9.0 | 6 930 | 0.235 | 1 695 |
| 材料 | γ | E /MPa | ρ/kg·m-3. | |||||
| 空气 | 1.4 | 0.25 | 1.239×10-3 | |||||
1.7 SPH模型的参数设置
在Visual Studio平台中使用Fortran 2003语言编写SPH算法程序,对颌面部软硬组织爆炸伤进行仿真运算。下颌骨、咬肌和TNT炸药的材料参数、爆炸状态方程、失效准则与FEM模型中相同,TNT爆点设置在炸药中心。对两侧髁突上的粒子进行约束,禁止其向任何方向自由移动。
2 结果 2.1 人下颌软硬组织FEM模型的建立建立了人下颌软硬组织爆炸伤的FEM实体网格模型,模型整体网格划分清晰、准确,几何外形与人体解剖结构相似(图 1)。建立的咬肌-下颌骨FEM模型的单元格数为34 687,节点数为9 257,模型单元格均为实体单元,最终得到的模型单元数及节点数见表 2。
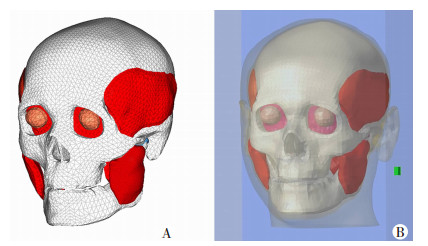
|
| A:人颌面部软硬组织FEM实体有限元网格模型肌肉(红色)、颌骨(白色); B:人颌面部软硬组织FEM爆炸伤模型肌肉(红色)、颌骨(白色)、空气域(蓝色)及TNT炸药(绿色) 图 1 人颌面部软硬组织FEM模型 |
| 材料 | 单元格 | 单元格节点 |
| 下颌骨皮质骨 | 14 132 | 3 476 |
| 下颌骨松质骨 | 5 435 | 2 212 |
| 左侧咬肌 | 15 120 | 3 569 |
| 空气(爆炸距离3 cm) | 1 105 920 | 1 138 489 |
| 炸药(1 000 mg) | 40 | 90 |
2.2 人下颌软硬组织SPH模型的建立
将实验中的咬肌-下颌骨软硬组织三维模型通过编程软件离散成SPH粒子,共得到4 538个粒子,设定粒子间距为3 mm,各粒子在三维空间中离散均匀分布。爆炸致伤条件为爆炸距离3 cm,TNT为1 000 mg,建立TNT炸药的粒子模型,并设定炸药粒子间距为0.5 mm,共得到粒子5 832个。成功建立了如图 2所示的下颌骨、咬肌组织爆炸损伤SPH粒子模型,共有粒子10 370个。
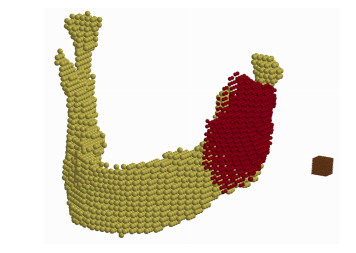
|
| 图 2 人下颌骨(黄色)、咬肌(红色)、TNT(棕色)爆炸伤SPH粒子模型 |
2.3 人下颌骨爆炸伤SPH与FEM模型应力分析
图 3为爆炸后0.100 ms时下颌骨的受力云图,结果显示:SPH模型中下颌骨应力最集中的区域为下颌角区、下颌乙状切迹、髁状突颈部,并导致这些区域骨折,这与FEM模型中结果一致。但是,下颌骨的最大应力分布区域与FEM模型中有一定的差别,主要表现为左侧下颌乙状切迹、髁突颈部应力集中面积小,下颌骨骨折不明显。
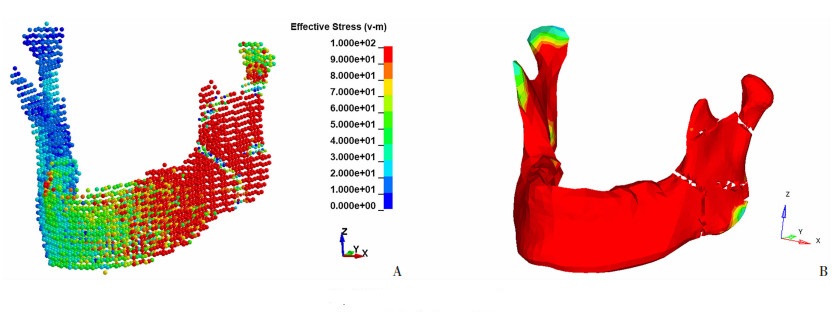
|
| A: SPH模型;B: FEM模型 图 3 爆炸距离3 cm、1 000 mg TNT爆炸后0.100 ms时下颌骨爆炸伤受力云图 |
2.4 咬肌爆炸伤SPH与FEM模型应力分析
图 4为爆炸后0.025 ms时咬肌的受力云图。结果显示:咬肌爆炸伤SPH模型中,咬肌粒子表现出贯穿性撕裂损伤,与FEM模型的差异主要表现为咬肌撕裂损伤表现不明显、咬肌应力分布区域降低。FEM仿真计算在100 μs时出现错误而导致运算中止,采用SPH方法后可仿真计算到6.7 ms。
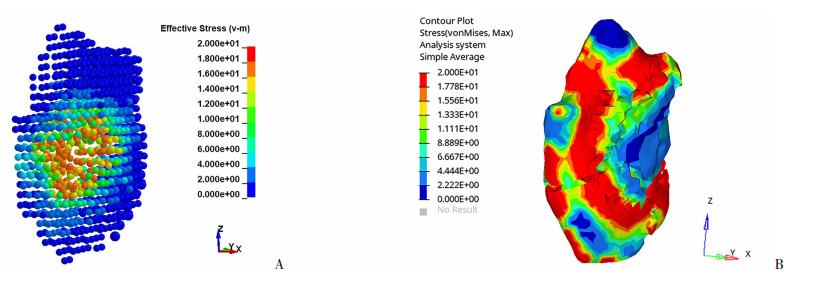
|
| A: SPH模型;B: FEM模型 图 4 爆炸距离3 cm、1 000 mg TNT爆炸后0.025 ms时咬肌爆炸伤受力云图 |
2.5 SPH与FEM模型应力-时间变化曲线分析
分别采用SPH和FEM方法建立咬肌和下颌骨应力-时间变化曲线(图 5)。结果显示:SPH模拟中,冲击波到达咬肌与下颌骨之后,应力值迅速增加,并很快到达最大值;FEM方法中,应力达到最大值之前有一段时间的应力波动,这是因为在FEM模拟中,计算不同单元格之间的相互作用时,使用了流固耦合与接触算法,而这两种算法都使用了非常复杂的边界处理方法,在极高应变速率下,非常容易导致应力波动,从而容易出现网格过度畸变。而在SPH算法中,仅需要通过核函数计算粒子间的相互作用,因此应力变化更稳定,在模拟爆炸伤对组织大变形、裂纹扩展具有优势。
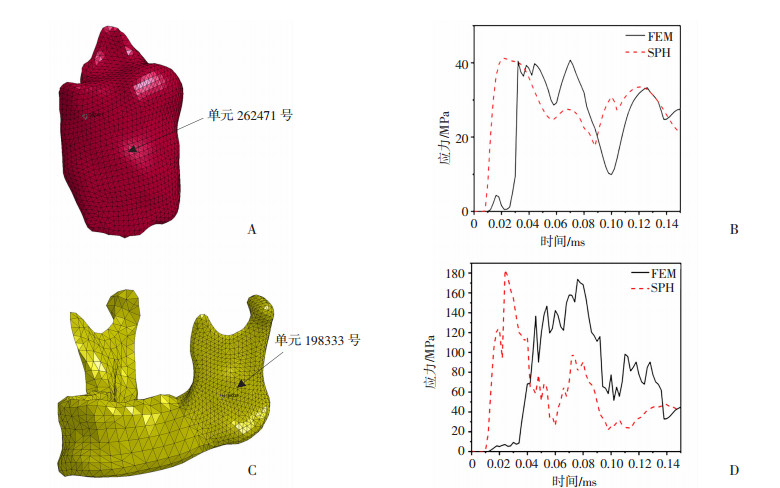
|
| A:左侧咬肌FEM模型箭头示选取的应力-时间分析点;B: FEM和SPH咬肌应力-时间变化曲线;C:下颌骨FEM模型箭头示选取的应力-时间分析点;D: FEM和SPH下颌骨应力-时间变化曲线 图 5 爆炸距离3 cm、1 000 mg TNT爆炸后咬肌、下颌骨爆炸伤应力-时间变化曲线 |
3 讨论
颌面部爆炸伤仿真研究中,常用的方法是FEM仿真模拟,其核心思想是将三维模型离散成连续的、有限的、形状规则的单元网格,然后对单元网格赋予的材料模型和材料参数,通过FEM软件来运算单元格在爆炸冲击波中的受力和变形情况,并且当某个单元格受力达到该单元格材料的失效准则时就会被删除,从而表现为下颌骨折和肌肉组织撕裂损伤。但是,随着对颌面部软硬组织模拟精度的要求越来越高,以及越来越复杂的致伤条件,FEM方法在爆炸损伤生物力学仿真中的局限性也越来越明显,甚至成为了限制颌面部软硬组织爆炸损伤生物力学中应用的关键因素[18-19]。
在颌面部软硬组织爆炸仿真中,冲击波载荷作用时间非常短,而在仿真运算时又必须将作用时间划分成更小的时间段,以便在更小的时间点内计算软硬组织单元格的受力和变形。如果单元格的刚度小,很容易在一个很小的时间段就发生非常显著的变形,这种大变形会导致两种后果:一是导致应力集中区域单元格极度畸变,从而导致爆炸损伤效果失真;二是使单元格极度扭曲变形产生负体积,从而使有限元仿真运算过程提前出现非正常终止[19]。特别是在肌肉等软组织运算中,由于软组织弹性模量小,在冲击波载荷下单元格产生非常大的变形,容易出现上述结果[20]。本研究中咬肌采用FEM爆炸仿真模拟即出现仿真停止现象。由于FEM方法的缺陷,所以在颌面部软组织的爆炸损伤仿真研究中,需要开发新的仿真方法。
SPH的基本思想是将复杂的颌面部软硬组织离散成空间内不连续的点阵,每个点阵称为粒子,因此,SPH方法又是一种无网格仿真方法[21]。无网格方法的基本思想是将连续的三维实体离散成有限个带质量的粒子,粒子之间不需要单元网格连接,而是通过计算函数将它们联系起来,物理性质全部分配在粒子上,由各个粒子表现出力学性质。粒子离散的好处是没有单元格的生成,从而避免了在FEM研究中单元格畸变和负体积而产生的影响。
爆炸是一个典型的大变形、高温、高压及高应变率的损伤,数值模拟为研究颌面部软硬组织爆炸伤提供了强有力的手段,能在时间和空间上更全面的获得生物力学信息。SPH在颌面部爆炸伤研究中有其独特的优势,不需要对模型进行划分网格,爆炸冲击波也不会使网格扭曲变形,因此SPH方法能够成功实现对颌面部软硬组织爆炸损伤的仿真[22]。为了研究SPH方法在颌面部软硬组织爆炸伤研究中的有效性,本研究通过SPH方法建立了人下颌骨硬组织、咬肌软组织的爆炸伤三维模型,并对该模型进行分析研究。人下颌占颌面部的1/2,是颌面部易受爆炸攻击的部位,爆炸伤发生概率较高。下颌角与颅脑、颈椎、咽、喉及舌根、眼、耳蜗等重要解剖结构相邻,爆炸伤后易并发颅脑、颈椎或上呼吸道损伤,导致伤员昏迷或休克。爆炸伤可导致舌体肿胀、舌根后坠,导致伤员呼吸困难;爆炸伤可致颈内外动静脉破裂导致颌面部大出血[23],因此,分析该下颌角区域爆炸伤的生物力学机制,对颌面部爆炸伤诊断、救治及防护有重要意义。
本研究结果显示SPH模型结构与人解剖结构相似,细节损失少,但是相对于FEM模型其逼真度欠佳,下颌骨和咬肌的解剖特点未表现出来,具体表现为未区分下颌骨骨皮质和骨松质,咬肌未表现出肌肉纤维排列特点。造成这些结果的主要原因一方面是通过SPH方法建立的人下颌骨、咬肌模型粒子数较少,如果将人下颌骨、咬肌进一步细化得到更多的粒子,其解剖形态和细节会更加逼真,但是粒子数目的增多会增加仿真模拟运算时间,本研究中仿真模拟运算时间为72 h。另一方面目前SPH无网格算法的研究还处于起步阶段,相关的研究较少,模拟分析软件还不够完善。本研究依据科学计算中常用的Fortran语言,编写SPH仿真算法对颌面部爆炸损伤进行仿真计算,然后将结果导入LS-PrePost后处理工具中进行分析,虽然取得一定的爆炸伤仿真模拟效果,但是该软件编程计算效率、计算精度以及稳定性方面还有待进一步研究。
本研究对爆炸损伤0.100、0.025 ms时下颌骨、咬肌受力云图进行分析,结果显示:通过SPH方法模拟的颌面部爆炸损伤主要导致左侧下颌角、髁状突骨折,咬肌广泛撕裂损伤,该仿真结果与FEM仿真结果接近。但是下颌骨的最大应力分布区域与FEM有一定的差别,主要表现为左侧下颌乙状切迹、髁突颈部应力集中面积小,下颌骨骨折不明显。咬肌爆炸伤SPH模型中,咬肌粒子表现出贯穿性撕裂损伤,并有一定程度的咬肌粒子反向飞溅,与FEM模拟的差异主要表现为咬肌撕裂损伤表现不明显,咬肌应力分布区域降低。这主要是由于SPH仿真方法与FEM方法对单元格失效的处理方式不同,在SPH仿真方法中,下颌骨和咬肌模型由离散的空间粒子组成,粒子与粒子之间存在相互作用力,当某个粒子因超过阈值导致失效时,该粒子并不会被删除,而是其与未发生失效的粒子之间不再有相互作用力,同时失效粒子之间仍然相互作用[13];而在有限元研究中,当单元的受力达到其设定的失效值,该单元会被删除,从而产生裂纹,当相邻的多个单元被删除时,就产生了明显的骨折线和咬肌撕裂损伤[24]。
本研究也存在一定的局限性:一方面,在爆炸冲击波致伤下颌骨和咬肌过程中,其应力分布面积相对较小,未能很好显示爆炸冲击波在不同组织界面中传播的特点,这主要是由于SPH是无网格算法,摆脱了对单元网格的依赖,仿真模拟被离散为有限个粒子,下颌骨、咬肌的变形通过粒子的力学运动来描述,虽然解决了传统有限元方法中的不足,但是SPH在计算每个粒子的能量变化时都需要用到临近粒子的信息,搜索临近粒子和计算粒子能量变化都比较困难,因此表现出应力分布面积相对较小;另一方面,本次模型中离散粒子数相对较少,但计算时间已是有限元模型的2倍左右,因此SPH方法的计算量过大也是其缺陷之一,如何提高计算效率一直是SPH研究所关心的问题。在以后的研究中,我们准备尝试将FEM和SPH方法的优点结合起来,建立FEM与SPH的耦合模型,在大部分受力较小的区域采用有限元网格,而在出现损伤和大变形的区域采用离散粒子,这样既能合理控制计算量,又能避免FEM和SPH方法各自的不足,还能改进计算结果与损伤效果。
综上所述,本研究采用SPH方法建立颌面部爆炸伤仿真模型,并与FEM方法进行对比研究,结果显示:SPH方法在颌面部软硬组织爆炸伤中对求解组织大形变、裂纹扩展、爆炸冲击等方面相对于FEM方法具有显著优势。SPH方法在颌面部软硬组织爆炸伤仿真研究中具有较好的应用前景。在今后研究中,可以将FEM和SPH两者的优点结合起来,建立FEM与SPH的耦合模型,对颌面部软硬组织爆炸伤的生物力学特点进行更加深入、细致的研究。
| [1] |
MATHEWS Z R, KOYFMAN A. Blast injuries[J]. J Emerg Med, 2015, 49(4): 573-587. DOI:10.1016/j.jemermed.2015.03.013 |
| [2] |
欧阳荣键, 朱勋志, 周旭华, 等. 人上颌骨爆炸冲击伤有限元仿真模拟及生物力学分析[J]. 军事医学, 2018, 42(8): 604-608, 615. OUYANG R J, ZHU X Z, ZHOU X H, et al. Biomechanical analysis of blast injury to human maxilla by finite element method[J]. Mil Med Sci, 2018, 42(8): 604-608, 615. DOI:10.7644/j.issn.1674-9960.2018.08.009 |
| [3] |
唐震, 周中华, 张绍祥, 等. 人下颌骨颏部正中位置枪弹伤的有限元动态模拟及分析[J]. 第二军医大学学报, 2011, 32(8): 845-850. TANG Z, ZHOU Z H, ZHANG S X, et al. Dynamic simulation and finite element analysis of gunshot wounds to the center of mandible mental region in human[J]. Acad J Second Mil Med Univ, 2011, 32(8): 845-850. |
| [4] |
周旭华, 朱勋志, 欧阳荣建, 等. 颌面部爆炸伤造成颅底继发损伤三维有限元仿真模拟及生物力学分析[J]. 第三军医大学学报, 2019, 41(4): 308-314. ZHOU X H, ZHU X Z, OUYANG R J, et al. Three-dimensional finite element simulation and biomechanical analysis of maxillofacial blast injuries and secondary injuries to the skull base[J]. J Third Mil Med Univ, 2019, 41(4): 308-314. DOI:10.16016/j.1000-5404.201810154 |
| [5] |
黄君杰, 徐帅, 季艳丹, 等. 人下颌角撞击伤造成颞下颌关节间接损伤的有限元模拟及生物力学分析[J]. 第三军医大学学报, 2020, 42(15): 1511-1518. HUANG J J, XU S, JI Y D, et al. Finite element simulation and biomechanical analysis of indirect injury of temporomandibular joint under lateral impact on the angle of human mandible[J]. J Third Mil Med Univ, 2020, 42(15): 1511-1518. DOI:10.16016/j.1000-5404.202003344 |
| [6] |
TADDEI L, FRISSANE H, LEBAAL N, et al. Smoothed particle hydrodynamics-based method for penetrating impacts in a biomechanical context[J]. Comput Methods Biomech Biomed Eng, 2017, 20(sup1): S199-S200. DOI:10.1080/10255842.2017.1382931 |
| [7] |
QIN Y, WU J H, HU Q M, et al. Computational evaluation of smoothed particle hydrodynamics for implementing blood flow modelling through CT reconstructed arteries[J]. J X-Ray Sci Technol, 2017, 25(2): 213-232. DOI:10.3233/xst-17255 |
| [8] |
LIU X M, WANG R Y, LI Y H, et al. Deformation of soft tissue and force feedback using the smoothed particle hydrod-ynamics[J]. Comput Math Methods Med, 2015, 2015: 1-10. DOI:10.1155/2015/598415 |
| [9] |
KULPER S A, FANG C X, REN X D, et al. Development and initial validation of a novel smoothed-particle hydrodynamics-based simulation model of trabecular bone penetration by metallic implants[J]. J Orthop Res, 2017, 36(4): 1114-1123. DOI:10.1002/jor.23734 |
| [10] |
TOMA M, NGUYEN P D H. Fluid-structure interaction analysis of cerebrospinal fluid with a comprehensive head model subject to a rapid acceleration and deceleration[J]. Brain Inj, 2018, 32(12): 1576-1584. DOI:10.1080/02699052.2018.1502470 |
| [11] |
MÜLLER M, SCHIRM S, TESCHNER M. Interactive blood simulation for virtual surgery based on smoothed particle hydrodynamics[J]. Technol Heal Care, 2004, 12(1): 25-31. DOI:10.3233/THC-2004-12103 |
| [12] |
LI S M, ABDEL-WAHAB A, DEMIRCI E, et al. Penetration of cutting tool into cortical bone: Experimental and numerical investigation of anisotropic mechanical behaviour[J]. J Biomech, 2014, 47(5): 1117-1126. DOI:10.1016/j.jbiomech.2013.12.019 |
| [13] |
FERNANDEZ J W, DAS R, CLEARY P W, et al. Using smooth particle hydrodynamics to investigate femoral cortical bone remodelling at the Haversian level[J]. Int J Numer Meth Biomed Engng, 2013, 29(1): 129-143. DOI:10.1002/cnm.2503 |
| [14] |
CHONG K, JIANG C, RAM D, et al. Visualization of vascular injuries in extremity trauma[J]. Med Biol Eng Comput, 2017, 55(9): 1709-1718. DOI:10.1007/s11517-017-1619-9 |
| [15] |
陈渝斌.下颌骨火器伤有限元仿真及生物力学机制的初步研究[D].重庆: 第三军医大学, 2010. CHEN Y B. Finite element analysis and preliminary investigation of biomechanical mechanism of wound ballistics of the mandible[D]. Chongqing: Third Military Medical University, 2010. |
| [16] |
MERKLE A C, WARD E E, O'CONNOR J V, et al. Assessing behind armor blunt trauma (BABT) under NIJ standard-0101.04 conditions using human torso models[J]. J Trauma, 2008, 64(6): 1555-1561. DOI:10.1097/TA.0b013e318160ff3a |
| [17] |
LEI T, XIE L X, TU W B, et al. Blast injuries to the human mandible: development of a finite element model and a preliminary finite element analysis[J]. Injury, 2012, 43(11): 1850-1855. DOI:10.1016/j.injury.2012.07.187 |
| [18] |
徐金中, 汤文辉. 空间碎片超高速碰撞问题的SPH方法模拟[J]. 强度与环境, 2008, 35(5): 25-31. XU J Z, TANG W H. Numerical simulation of hypervelocity impacts of space debris using SPH method[J]. Struct Environ Eng, 2008, 35(5): 25-31. |
| [19] |
卞梁.高速碰撞中的SPH方法及其应用研究[D].合肥: 中国科学技术大学, 2009. BIAN L. The SPH method and its application in hypervelocity impact[D]. Hefei: University of Science and Technology of China, 2009. |
| [20] |
韩旭, 伍乾坤, 胡德安. SPH方法模拟高速碰撞问题的实例[C]//计算爆炸力学进展.青岛: 中国力学学会爆炸力学专业委员会, 2006: 240-245. HAN X, WU Q K, HU D A. Examples of SPH method to simulate high-speed collision problems[C]//Update in computational explosion mechanics. Qingdao: Professional Committee of Explosive Mechanics, Chinese Society of Mechanics, 2006: 240-245. |
| [21] |
SHAHRIARI S, GARCIA D. Meshfree simulations of ultrasound vector flow imaging using smoothed particle hydrodynamics[J]. Phys Med Biol, 2018, 63(20): 205011. DOI:10.1088/1361-6560/aae3c3 |
| [22] |
SIGALOTTI L D G, TROCONIS J, SIRA E, et al. Smoothed particle hydrodynamics simulations of evaporation and explosive boiling of liquid drops in microgravity[J]. Phys Rev E, 2015, 92: 013021. DOI:10.1103/physreve.92.013021 |
| [23] |
GATAA I S, MUASSA Q H. Patterns of maxillofacial injuries caused by terrorist attacks in Iraq: retrospective study[J]. Int J Oral Maxillofac Surg, 2011, 40(1): 65-70. DOI:10.1016/j.ijom.2010.07.005 |
| [24] |
MONAGHAN J J. Smoothed particle hydrodynamics[J]. Annu Rev Astron Astrophys, 1992, 30(1): 543-574. DOI:10.1146/annurev.aa.30.090192.002551 |



