2. 400042 重庆,重庆市疾病预防控制中心;
3. 610500 成都,成都医学院卫生统计学教研室
2. Chongqing Center for Disease Control and Prevention, Chongqing, 400042;
3. Department of Health Statistics, Chengdu Medical College, Chengdu, Sichuan Province, 610500, China
自1993年重庆市发现首例HIV感染者以来,重庆市HIV/AIDS病例数量逐年增多,流行范围迅速扩大,流行速度显著加快。同时相比其他传染病,艾滋病具有潜伏期长、传播途径隐秘(常通过吸毒、性行为传播)等特征,常规监测方法不能获得准确的疫情信息。因此,利用已掌握的有限信息,运用数学和流行病学模型等方法对其疫情进行科学估计和预测,就显得尤为重要[1]。利用数学模型预测艾滋病的方法有多种,但是这些预测模型对重庆市艾滋病疫情预测的效果尚需要进行探索和比较分析。本研究选择重庆市2006-2015年期间的新发报告人数进行拟合,并以2016-2017年新发报告人数进行预测和验证。通过构建并比较适合于重庆市艾滋病疫情的模型和预测方法,为制定艾滋病有效的防控措施提供科学合理的理论依据。
1 资料与方法 1.1 资料来源收集的数据主要来源于重庆市疾病预防控制中心艾滋病综合防治数据信息系统的监测数据。评价指标为1995年1月1日至2015年12月31日期间HIV/AIDS病例的新发报告数,入选标准是现住址为重庆市的新发病例。人口学数据来自于重庆市统计年鉴。本研究经第三军医大学医学伦理委员会审核(20140410)。
1.2 模型方法采用ARIMA模型、指数平滑法和趋势外推法3种常见的时间序列模型对2006-2015年重庆市新报告的HIV/AIDS病例总数进行拟合,对2016和2017年的新报告HIV/AIDS病例数进行预测并验证。
1.2.1 ARIMA模型建立ARIMA模型将随时间变化的数据序列列为随机序列,这组随机变量中存在的依存关系受到外部因素和自身变动规律的影响,反映了在时间变化发展过程中原始数据的延续性[2]。在SPSS中对2006-2015年重庆市艾滋病月发病数序列的时间定义为年-月份型,起始点为2006年1月。绘制时间序列图,通过时间序列图观察其平稳性,若序列呈现非平稳性,则需要通过数据转换、差分和季节差分,使之成为无趋势的平稳序列。根据该时间序列是否存在月的周期性变化,选择构建季节性ARIMA(p, d, q)(P, D, Q)S或非季节性ARIMA(p, d, q)。通过分析自相关函数图(ACF)及偏自相关函数图(PACF)确定模型参数p、d、q、P、D、Q值,并初步选出几个模型以作进一步分析。
先对初步选定的模型中的参数作假设检验,若Box-Ljung统计量检验差异无统计学意义,即残差为随机的、白噪声序列。若几个模型的参数检验都无统计学意义(即均为白噪声序列),则以模型中贝叶斯信息准则(BIC)值最小作为指标来选择最佳模型。若残差序列不是白噪声序列,则需要重新进行模型识别,调整模型参数,再进行模型诊断。在模型的实际应用中,模型诊断是一个不断完善的过程,为了提高模型拟合的精度,需要不断调整参数[3]。基于2006-2015年重庆市HIV/AIDS月新发报告数据建立最优模型,用2016年和2017年的实际数据对模型的预测效果进行验证。
1.2.2 指数平滑法建立指数平滑法基本思想是利用序列过去值的加权平均数来预测其未来值,并通过权重的大小来反映不同时期间对结果影响的大小。在SPSS中对2006-2015年重庆市艾滋病月发病数序列的时间定义为年-月份型,起始点为2006年1月。绘制时间序列图,通过时间序列图观察其平稳性,若序列呈现非平稳性,则需要通过数据转换、差分和季节差分,使之成为无趋势的平稳序列。通过观察时间序列图,根据该时间序列是否存在季节性变化,选择非季节性指数平滑法(包括简单性指数平滑法、Brown单参数线性指数平滑法、Holt双参数指数平滑法)和季节性指数平滑法(简单季节性指数平滑法、Winter可加性指数平滑法、Winter可乘性指数平滑法)。对选定的几种模型根据均方根误差(RMSE)和平均绝对误差百分比(MAPE)最小原则确立最优模型。对所建立的模型进行残差检验,即Box-Jenkins统计量检验无统计学意义,残差应是随机的,为白噪声。若残差序列不是白噪声序列,则需要重新调整模型参数,再进行模型诊断。基于2006-2015年重庆市HIV/AIDS月新发报告数建立相关模型,用2016和2017年的实际数据对模型的预测效果进行验证。
1.2.3 趋势外推法建立从疾病预测的原理上讲,趋势外推法属于因果分析方法,即未来是过去和现在连续发展的结果,通过一条函数曲线来寻找一个指标和其他指标间的规律性关系,为预测未来提供依据[4]。在SPSS中对2006-2015年重庆市HIV/AIDS新发报告数序列以年份为自变量,HIV/AIDS新发报告数为因变量,起始点为2006年,绘制散点图,观察数据分布特征是否适用于趋势外推模型。根据散点图发现HIV/AIDS新发报告数与时间之间呈非线性关系,而趋势外推法包括一次曲线、增长曲线、二次曲线、复合曲线、三次曲线、对数曲线、指数曲线、逆模型、S曲线、幂函数模型、Logistic模型共11中曲线模型[5]。采用合适的曲线模型作趋势外推。在模型假设检验有统计学意义的前提下,对选定的几种模型以决定系数越大,标准误差越小的原则选取最优模型。按照选定的最优曲线模型公式计算2016和2017年的预测结果,并与2016和2017年的实际数据进行验证。
1.2.4 3种模型拟合效果和预测效果的比较3种模型的拟合精度主要通过标准误差进行比较,对近2年的预测效果则通过平均相对误差来进行比较。
1.3 统计学分析使用Excel 2010进行数据整理和分析;采用SPSS 20.0 ARIMA模型、指数平滑法和趋势外推法3种常见的时间序列模型统计软件对模型进行拟合和预测分析,检验水准:α=0.05。
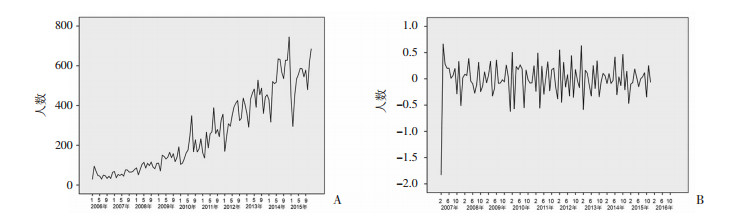
2 结果 2.1 ARIMA模型对重庆市HIV/AIDS新发报告总数的预测结果 2.1.1 序列平稳化以2006年1月至2015年12月的新发报告总数作时间序列图(图 1A)。为去除趋势性和季节性因素的影响,对原始数据序列通过取自然对数变换,一阶差分和一阶季节差分后,序列近似平稳,满足序列平稳化的要求,变换后的序列见图 1B。
|
| A:数据变换前;B:数据变换后 图 1 重庆市HIV/AIDS新发报告总数序列数据变换前后 |
2.1.2 模型识别
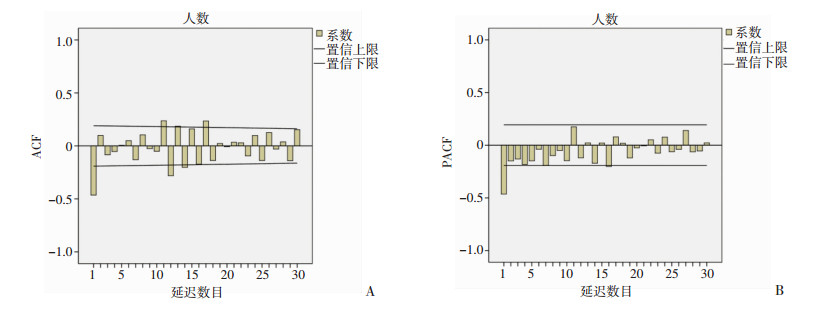
观察数据变换后的ACF和PACF图(图 2),模型中的d和D应同时取为1;从ACF图看,在1阶之后函数值明显趋于0,呈截尾性,是以可将q取为1,而第12阶的函数值显著不为0,是以可将Q取为1;再看PACF图,1阶之后函数值趋于0并呈拖尾性,是以可将p取为1,P取为0,再通过低阶向高阶逐个比较,选择进一步分析的模型为:ARIMA(1, 1, 1)(0, 1, 0)、ARIMA(1, 1, 1)(0, 1, 1)、ARIMA(0, 1, 1)(0, 1, 0)、ARIMA(0, 1, 1)(0, 1, 1)。
|
| 图 2 ARIMA模型数据变换后的ACF(A)和PACF(B) |
2.1.3 模型诊断
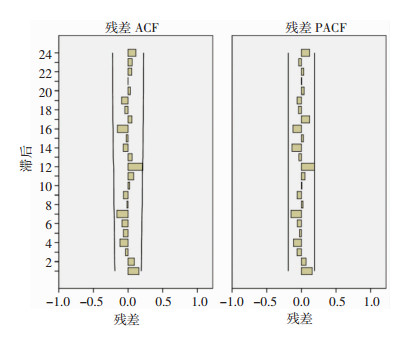
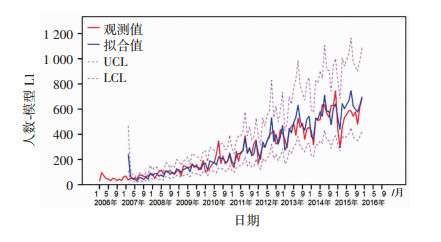
对4个备选模型进行构建,通过Ljung-Box Q统计量的假设检验结果可知:4个备选模型均无统计学意义,符合ARIMA模型建模要求。进一步比较备选模型的BIC值,ARIMA(0, 1, 1)(0, 1, 1)模型的RMSE为62.30,MAPE为21.86%,R2和BIC值分别为0.892和8.395,其BIC值最小(表 1)。从图 3 ARIMA(0, 1, 1)(0, 1, 1)模型的残差ACF和PACF图可见,残差序列是平稳的。因此,选择ARIMA(0, 1, 1)(0, 1, 1)模型为最佳模型。运用该模型拟合2006-2015年的流行趋势,模型拟合值的变化趋势与实际值基本吻合,各月份的实际报告数均落在了拟合值的置信区间内,见图 4。说明ARIMA(0, 1, 1)(0, 1, 1)模型对HIV/AIDS患者新发报告数的拟合情况比较良好。
| 模型 | R2 | BIC | L | P值 |
| ARIMA(1, 1, 1)(0, 1, 0) | 0.845 | 8.758 | 16.573 | 0.414 |
| ARIMA(1, 1, 1)(0, 1, 1) | 0.895 | 8.427 | 17.902 | 0.268 |
| ARIMA(0, 1, 1)(0, 1, 0) | 0.848 | 8.690 | 17.110 | 0.447 |
| ARIMA(0, 1, 1)(0, 1, 1) | 0.892 | 8.395 | 21.587 | 0.157 |
| R2为决定系数,BIC为贝叶斯信息准则,L为统计量 | ||||
|
| 图 3 ARIMA(0, 1, 1)(0, 1, 1)模型的残差ACF(A)和PACF(B) |
|
| 图 4 ARIMA(0,1,1)(0,1,1)模型的拟合值和实际值序列 |
2.1.4 模型预测
运用ARIMA(0, 1, 1)(0, 1, 1)模型预测2016年新发总人数为7 376人,比实际值(7 058)多318人,相对误差为4.51%。预测2017年新发总人数为8 017人,比实际值(7 672)多345人,相对误差为4.50%。
2.2 指数平滑法对重庆市HIV/AIDS新发报告总数的预测结果 2.2.1 模型预处理由于指数平滑法使用的数据和ARIMA模型的数据是同一数据,因此对HIV/AIDS的新发报告总数绘制序列图(图 1A)。HIV/AIDS新发报告数总体呈现明显的上升趋势,但无法确定有无季节周期性。经过自然对数转换,一阶差分和一阶季节差分后,序列基本平稳(图 1B),说明该序列有季节周期性。
2.2.2 模型识别根据季节性特点和不同指数平滑法的特征,初步选用简单季节性指数平滑法、Winters可加性指数平滑法和Winters可乘性指数平滑法进行模型拟合。
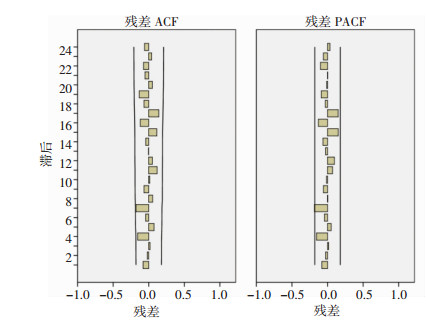
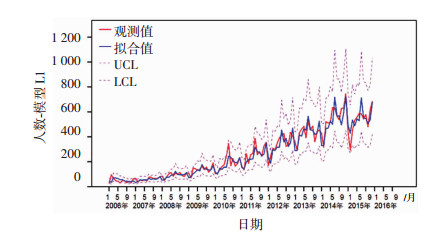
2.2.3 模型诊断以HIV/AIDS的月新发病数为因变量的3种不同指数平滑法,对3种模型进行参数比较(表 2)。根据RMSE、MAPE最小原则,简单季节性指数平滑法的RMSE为45.51,MAPE为15.16%,是3种预测模型中数值最小的。从图 5简单季节性指数平滑法的残差的ACF和PACF图可见,残差序列是平稳的。对简单季节性指数平滑法进行残差检验,P值0.233,无统计学意义,即残差为白噪声。因此最佳模型为简单季节性指数平滑法。根据图 6的模型拟合序列图可见,模型拟合值的变化趋势与实际值基本吻合,各月份的实际新发报告数均落在了预测值的置信区间内,说明简单季节性指数平滑法对HIV/AIDS患者新发报告数的拟合情况比较良好。
| 指数平滑法 | 拟合统计量 | Ljung-Box Q方法 | |||
| 标准误差 | 平均绝对误差百分比(%) | 统计量 | P值 | ||
| 简单季节性 | 45.51 | 15.16 | 19.719 | 0.233 | |
| Winters可加性 | 50.72 | 15.61 | 16.703 | 0.337 | |
| Winters可乘性 | 62.79 | 18.39 | 18.274 | 0.249 | |
|
| 图 5 简单季节性指数平滑法的残差ACF(A)和PACF(B) |
|
| 图 6 简单季节性模型的拟合值和实际值序列 |
2.2.4 模型预测
采用简单季节性指数平滑法对重庆市HIV/AIDS患者新发报告发病数进行预测,预测2016年新发总人数为7 070人,比实际值(7 058人)多12人,相对误差为0.17%;预测2017年新发总人数为7 373人,比实际值(7 672人)少299人,相对误差为3.90%。
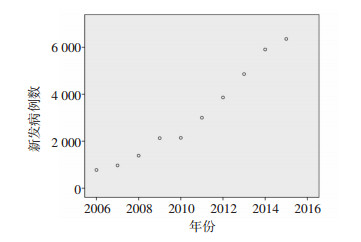
2.3 趋势外推法对重庆市HIV/AIDS新发报告总数的预测结果 2.3.1 模型预处理首先绘制2006-2015年新发报告数随时间序列的散点图(图 7)。
|
| 图 7 重庆市HIV/AIDS新发报告总数随时间变化的散点图 |
2.3.2 模型识别
观察散点图发现HIV/AIDS新发报告数与时间之间呈非线性关系,不确定哪种模型最合适,因此运用11种曲线模型对该时间序列进行趋势外推。
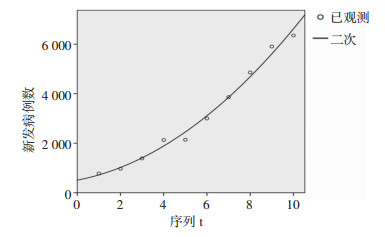
2.3.3 模型诊断在模型假设检验有统计学意义(P < 0.05)的前提下,模型拟合优度参数的比较以决定系数越大,标准误差越小的原则(表 3)。二次曲线模型和三次曲线模型的决定系数基本相同,且均有统计学意义(P < 0.05),但是二次曲线模型的标准误差较小,而模型假设检验统计量F值更大,因此提示二次曲线模型能更好地拟合重庆市2006-2015年新发报告总数的变化趋势(图 8)。二次曲线模型中各系数及其假设检验结果见表 4。根据表 4的结果数据,建立新报告数的拟合模型方程: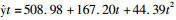
| 方法 | 模型摘要 | 模型假设检验 | |||||
| 相关系数 | 决定系数 | 调整的决定系数 | 标准误差 | F值 | P值 | ||
| 二次曲线 | 0.995 | 0.990 | 0.987 | 227.29 | 353.163 | 0.000 | |
| 三次曲线 | 0.996 | 0.992 | 0.987 | 228.46 | 233.333 | 0.000 | |
| 复合曲线 | 0.990 | 0.981 | 0.978 | 0.11 | 402.975 | 0.000 | |
| 增长曲线 | 0.990 | 0.981 | 0.978 | 0.11 | 402.975 | 0.000 | |
| 指数曲线 | 0.990 | 0.981 | 0.978 | 0.11 | 402.975 | 0.000 | |
| Logistic函数 | 0.990 | 0.981 | 0.978 | 0.11 | 402.975 | 0.000 | |
| 一次曲线 | 0.981 | 0.962 | 0.957 | 418.63 | 202.265 | 0.000 | |
| 幂函数 | 0.970 | 0.940 | 0.933 | 0.19 | 125.594 | 0.000 | |
| 对数曲线 | 0.883 | 0.780 | 0.753 | 1006.26 | 28.392 | 0.001 | |
| S曲线 | 0.845 | 0.715 | 0.679 | 0.42 | 20.045 | 0.002 | |
| 逆曲线 | 0.705 | 0.497 | 0.434 | 1522.87 | 7.889 | 0.023 | |
|
| 图 8 重庆市HIV/AIDS新发报告总数二次曲线模型拟合图 |
| 公式对应值 | 未标准化系数 | 标准化系数 Beta |
t值 | P值 | |
| β | SE | ||||
| ln(t) | 167.20 | 111.65 | 0.25 | 1.50 | 0.178 |
| ln(t)2 | 44.39 | 9.89 | 0.75 | 4.49 | 0.003 |
| a | 508.98 | 267.32 | 1.90 | 0.099 | |
| a:常数项;β: Beta:系数;SE:标准误;t:年份 | |||||
2.3.4 模型预测
二次曲线模型的决定系数为0.990,标准误差为227.29,其预测方程为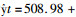
以上分别运用ARIMA模型、指数平滑法和趋势外推法对2006-2015年期间重庆市HIV/AIDS新发报告总数进行了拟合预测(表 5),提示简单季节性指数平滑法拟合2006-2015年重庆市HIV/AIDS新发报告总数效果更好、能更准确的预测重庆市HIV/AIDS新发总人数。
| 预测模型 | 预测模型有效性 | 标准误差 | 2016年的相对误差/% | 2017年的相对误差/% | 2016和2017的平均相对误差/% |
| ARIMA模型 | 有效 | 62.30 | 4.51 | 4.50 | 4.51 |
| 指数平滑法 | 有效 | 45.51 | 0.17 | 3.90 | 2.04 |
| 趋势外推法 | 有效 | 227.29 | 9.37 | 16.11 | 12.74 |
3 讨论
如何准确、有效地预测艾滋病疫情的发展是艾滋病的防治工作中一项重要的工作。随着预测理论的逐步完善和预测技术的不断发展,许多新的统计模型和预测方法被应用到艾滋病的预测中。艾滋病在不同地区不同时间其流行特征也不一样,对单一因素的分析并不能够全面掌握艾滋病的流行规律和特征。有研究证明,人口、经济、环境、气候及行为等流行因素的变化均与时间之间存在紧密的联系[6]。
时间序列分析是对变量随时间发展变化的一种研究,并利用以往的统计数据建立外推预测方法的数学模型。主要包括ARIMA法、指数平滑法和趋势外推法等。但由于各类模型的应用条件不同,对同样的疫情报告数据用不同的预测模型拟合时,其准确性也可能不尽相同。
ARIMA模型综合考虑了序列的趋势性和周期性变化,通过对模型参数的定量表达,对时间序列先作假设验证,并可通过模型识别对模型进行迭代修改以获得最佳模型。由于ARIMA模型的模型参数组合很多,需要先根据时间序列图、自相关函数图(ACF)和偏相关函数图(PACF)来初步选择几个模型,再通过模型拟合优度的结果来确定最优模型。该模型是一种大幅提高精度的短期预测方法,是目前最常用的时间序列模型[2, 7],在多个领域得到广泛的应用。本研究中ARIMA模型可以对重庆市HIV/AIDS的新发报告总数进行预测。运用ARIMA(0, 1, 1)(0, 1, 1)模型预测2016年新发总人数为7 376人,比实际值(7 058人)多318人,相对误差为4.51%。预测2017年新发总人数为8 017人,比实际值(7 672人)多345人,相对误差为4.50%。指数平滑法主要是通过对实际数据进行加权来获取预测值,它是根据数据的时间远近赋予大小不等的权重,以使预测结果更为合理[8]。指数平滑法是为了消除随机的一部分变化,从而找出其中蕴含的规律性,以便合理的预测未来的发展趋势。指数平滑法按变化趋势和季节特点分为多种模型,在实际应用当中,需要根据不同的适用范围,即数据是否存在趋势变化、季节变化等特点选择合适的模型。本研究中简单季节性指数平滑法对重庆市HIV/AIDS的新发报告总数拟合和预测效果更好,提示了简单季节性指数平滑法能够更好、更准确的拟合和预测艾滋病的发病情况,可以为艾滋病的防治工作提供一定的科学佐证。这与谢妮等[9]对深圳市艾滋病疫情的预测研究相一致。当原始数据表现出一定的随机性和平稳性时,采用指数平滑法分析往往能取得较好的效果,但是当数据呈现出非随机性和非平稳性时,即使经过数据变化处理后平稳,依然难以达到最优条件,这就会导致模型的拟合效果不甚理想。
趋势外推法对数据要求不高,即使样本量较少,效果依然比较好[10-11],国内研究有马玉秀[12]运用GM(1, 1)模型、趋势外推法以及两者的组合模型预测传染病发病率,龚磊等[13]利用趋势外推法对流行性感冒的发病预测,结果均比较可靠。本研究中趋势外推法对HIV/AIDS的新发报告总数拟合效果及预测效果比较差(标准误差为228.46,平均相对误差为12.74)。趋势外推法常用于较长期的预测分析,但对于波动性较大的序列不适合做精确预测。较强的主观性使得模型选择上的差异会导致对同批数据不同的分析结论。在应用趋势外推法进行预测时应当注意,只有通过对曲线预测模型的检验和对预测误差的计算,曲线预测模型才能用于实际预测[5]。
ARIMA模型、指数平滑法和趋势外推法3种预测模型对重庆市新发报告总数的拟合效果和预测效果不同,不能简单地认为哪种模型好或者不好,在不同条件下选择模型拟合时,要根据实际的情况选择各类模型的最优模型[14]。无论哪种时间序列模型都是利用一维的时间序列资料,在模型预测中突出时间因素的作用,不需要考虑其他相关因素的影响,这是其优势所在。但同时也应注意到,正是由于未考虑其他相关因素的影响,它也有一定的局限性。当外界其他相关因素发生较大变化时,预测结果往往会产生较大的偏差[15]。对于目前大多数的预测模型,均是在没有其他相关因素干扰的前提下进行预测,而艾滋病的流行趋势受到很多因素的影响,如社会经济发展、社会行为改变、人口流动性及医疗技术突破等[16],如果政府加强对高危人群的宣传教育、对吸毒人群进行管控、公安对职业性工作者打击力度增大、农民群体人口流动性变小、艾滋病的治疗药物突破等情况出现,就会导致所研究对象的趋势发生改变,则必须积累新的数据以便对预测模型进行修正或重新拟合,才能达到更好更准确的预测效果。
| [1] |
王超, 贾忠伟, 郭秀花, 等. HIV/AIDS疫情发生与进展的预测方法[J].
北京医学, 2010, 32(12): 993–996.
WANG C, JIA Z W, GUO X H, et al. Prediction methods of HIV/AIDS epidemic occurrence and progress[J]. Beijing Med J, 2010, 32(12): 993–996. DOI:10.15932/j.0253-9713.2010.12.014 |
| [2] |
博克斯, 詹金斯, 莱因泽尔.时间序列分析: 预测与控制[M].王成璋, 尤梅芳, 郝杨, 译.北京: 机械工业出版社, 2011: 51.
BOX G E P, JENKINS G M, REINSEL G C. Time series analysis: forecasting and control[M]. WANG C Z, YOU M F, HAO Y, Translated.Beijing: China Machine Press, 2011: 51. |
| [3] |
范引光, 吕金伟, 戴色莺, 等. ARIMA模型与灰色预测模型GM(1, 1)在HIV感染人数预测中的应用[J].
中华疾病控制杂志, 2012, 16(12): 1100–1103.
FAN Y G, LYU J W, DAI S Y, et al. Prediction on the number of HIV with models of ARIMA and GM (1, 1)[J]. Chin J Dis Control Prev, 2012, 16(12): 1100–1103. |
| [4] |
杨永利, 毛赛彩, 薛源, 等. GM(1, 1)和趋势外推模型在我国艾滋病发病率预测中的应用[J].
中国卫生统计, 2014, 31(6): 952–954.
YANG Y L, MAO S C, XUE Y, et al. Prediction on the incidence rate of AIDS in China with gray model(1, 1) and trend extrapolation model[J]. Chin J Health Stat, 2014, 31(6): 952–954. |
| [5] |
薛薇. SPSS统计分析方法及应用[M]. 3版. 北京: 电子工业出版社, 2013.
XUE W. SPSS statistical analysis method and application[M]. 3 Ed. Beijing: Electronic Industry Press, 2013. |
| [6] |
吴家兵, 叶临湘, 尤尔科. 时间序列模型在传染病发病率预测中的应用[J].
中国卫生统计, 2006, 23(3): 276.
WU J B, YE L X, YOU E K. Application of time series model in prediction of incidence rate of infectious diseases[J]. Chin J Health Stat, 2006, 23(3): 276. DOI:10.3969/j.issn.1002-3674.2006.03.037 |
| [7] |
丁亚兴, 张之伦, 朱向军. 自回归综合移动平均模型对天津市甲型肝炎发病预测[J].
疾病监测, 2008, 23(5): 326–328.
DING Y X, ZHANG Z L, ZHU X J. Prediction of the incidence of hepatitis A in Tianjin using the autoregressive integrated moving average model[J]. Dis Surveillance, 2008, 23(5): 326–328. DOI:10.3784/j.issn.1003-9961.2008.05.024 |
| [8] |
王昕, 程小雯, 房师松, 等. 指数平滑模型在流感样病例预测中的应用[J].
中国热带医学, 2011, 11(8): 938–939.
WANG X, CHENG X W, FANG S S, et al. Application of exponential smoothing model in forecasting influenza incidence[J]. China Tropical Med, 2011, 11(8): 938–939. DOI:10.13604/j.cnki.46-1064/r.2011.08.023 |
| [9] |
谢妮.深圳市HIV/AIDS疫情分布特征与预测模型比较[D].长沙: 中南大学, 2011.
XIE N. The epidemic character of HIV/AIDS and comparison of different prediction models in Shenzhen[D]. Changsha: Central South University, 2011. |
| [10] | YU Z C, ZHANG W X, CHEN H, et al. Limited sampling strategy for the estimation of mycophenolic acid area under the plasma concentration-time curve in adult patients undergoing liver transplant[J]. Ther Drug Monit, 2007, 29(2): 207–214. DOI:10.1097/FTD.0b013e318040ce0b |
| [11] | EARNEST A, CHEN M I, NG D, et al. Using autoregressive integrated moving average (ARIMA) models to predict and monitor the number of beds occupied during a SARS outbreak in a tertiary hospital in Singapore[J]. BMC Health Serv Res, 2005, 5: 36. DOI:10.1186/1472-6963-5-36 |
| [12] |
马玉秀. 2006-2015年济南市槐荫区法定传染病流行趋势及预测分析[D].济南: 山东大学, 2016.
MA Y X. The analysis and predicting of trend of notifiable infectious diseases in Huaiyin from 2006-2015[D]. Jinan: Shangdong University, 2016. |
| [13] |
龚磊, 吴家兵, 侯赛, 等. 曲线估计在流行性感冒发病预测中的应用[J].
华南预防医学, 2017, 43(1): 30–33.
GONG L, WU J B, HOU S, et al. Application of curvilinear estimation in predicting incidence of influenza[J]. South China J Prev Med, 2017, 43(1): 30–33. DOI:10.13217/j.scjpm.2017.0030 |
| [14] |
朱宗元, 于青. ARIMA模型在我国病毒性肝炎发病率预测中的应用[J].
中国卫生统计, 2011, 28(1): 65–67.
ZHU Z Y, YU Q. Application of ARIMA model in predicting the incidence of viral hepatitis in China[J]. Chin J Health Stat, 2011, 28(1): 65–67. DOI:10.3969/j.issn.1002-3674.2011.01.022 |
| [15] |
赛晓勇, 张治英, 徐德忠, 等. 不同时间序列分析法在洞庭湖区血吸虫病发病预测中的比较[J].
中华流行病学杂志, 2004, 25(10): 863–866.
SAI X Y, ZHANG Z Y, XU D Z, et al. Application of "time series analysis" in the prediction of schistosomiasis prevalence in areas of "breaking dikes or opening sluice for waterstore" in Dongting Lake areas, China[J]. Chin J Epidemiol, 2004, 25(10): 863–866. DOI:10.3760/j.issn:0254-6450.2004.10.010 |
| [16] |
董蒴, 廖小勇, 任全玉. 艾滋病预测模型及其应用研究-基于灰色系统理论[J].
现代商贸工业, 2011(8): 25–26.
DONG S, LIAO X Y, REN Q Y. Research on AIDS prediction model and its prediction based on grey system theory[J]. Mod Bus Trade Ind, 2011(8): 25–26. DOI:10.3969/j.issn.1672-3198.2011.08.015 |



